流体静力学基础

气体性质

压缩性

体积弹性模数

定义：产生单位相对体积变化所需压强增高
$$
E=-\frac{dp}{dV/V}
$$
对于一定质量气体，体积与密度成反比例关系，即
$$
\frac{d \rho}{\rho}=-\frac{dV}{V}
$$
回代得
$$
E=\rho \frac{dp}{d \rho}
$$
常温下水的体积弹性模数：$2.1 \times 10^9N/m^2$
通常情况下水可视为不可压缩流体。

粘性

牛顿粘性定律

流体运动所产生的摩擦阻力与接触面积成正比
$$
\tau =\mu \frac{du}{d \vec{n}}
$$
$\tau$ ：摩阻应力，单位面积上的摩擦阻力
$\vec{n}$ ：接触面法线方向
$\mu$ ：比例常数，称为流体的粘性系数，单位为 $N \cdot s/m^2$
$\frac{du}{d \vec{n}}$ ：速度梯度

不同流体介质粘性系数值各不相同，并且粘性系数随温度变化，与压强基本无关。
气体粘性系数随温度升高而增大。

萨特兰公式

空气粘性系数随温度变化关系，近似公式之一萨特兰公式
$$
\frac{\mu}{\mu_0}=(\frac{T}{288.15})^{1.5}\frac{288.15+C}{T+C}
$$
$\mu_0$ ：温度为 $288.15K$ 时空气粘性系数
$C$ ：常数，值为 $110.4K$

运动粘性系数

$$
\nu=\frac{\mu}{\rho}
$$
$\nu$ ：运动粘性系数，单位为 $m^2/s$
$\mu$ ：粘性系数
$\rho$ ：密度

传热性

定义：当气体中沿某一方向存在温度梯度时，热量就会由温度高的地方传向温度低的地方，这种性质称为气体的传热性。
单位时间内所传递热量与传热面积成正比，与沿热流方向的温度梯度成正比，即
$$
q=-\lambda \frac{\partial T}{\partial \vec{n}}
$$
$q$ ：单位时间通过单位面积热量，单位 $kJ/(m^2 \cdot s)$
$\frac{\partial T}{\partial \vec{n}}$ ：温度梯度，单位为 $K/m$
$\lambda$ ：导热系数，单位为 $kJ/(m \cdot K \cdot s)$
负号表示热量传递方向永远与温度梯度方向相反。

流体分类

连续介质假设

理想流体

不考虑粘性，在这种模型中，流体微团不承受粘性力作用。常用于气体。
忽略粘性的气体称为理想气体。

压强各向同性

理想流体内一点处的压强与受压面的方位无关，它仅是空间坐标的连续函数。

不可压流体

不考虑气体压缩性或弹性，可认为体积弹性模数无穷大，或流体密度为常数。常用于液体。
求解不可压流体的流动规律，只需要服从力学定律，不需要考虑热力学关系。

对流速较低的气体，也可按不可压流体处理流动问题。

绝热流体

不考虑流体传热性的模型，即把流体热导系数看作零。低速流动的空气一般热导系数值很小，可视为绝热。
不考虑气体微团之间热传导作用的气体模型称之为绝热气体。

完全气体

任何状态下，气体的压强、密度和温度之间都存在一定的函数关系
$$
p=p(\rho,T)
$$

完全气体的状态方程

$$
p=\frac{\overline{R}}{m}\rho T
$$
$\overline{R}$ ：普适气体常数，$8315m^2/(s^2 \cdot K)$
$m$ ：某种气体相对分子质量
$R=\frac{\overline{R}}{m}$ 时，
$$
p=\rho R T
$$
$R$ 为气体常数，空气约为 $287.035m^2/(s^2 \cdot K)$

流体微团受力

压力

切应力（摩擦力）

彻体力

• 重力
• 电磁力
• 离心力

静平衡方程

在==静止流体==中取一点 $P$，压强为 $p$
构建笛卡尔坐标系，流体内各点处压强为
$$
p(x,y,z)
$$
以 $P$ 为中心构建各边平行于坐标轴的长方体，边长为 $dx,dy,dz$
观察 $x$ 轴方向，两面受压力大小分别为
$$
[p(x_0,y_0,z_0)+(\frac{\partial p}{\partial x})(\frac{dx}{2})]dx dy
$$
$$
[p(x_0,y_0,z_0)-(\frac{\partial p}{\partial x})(\frac{dx}{2})]dx dy
$$

流体微团 $x$ 轴方向受彻体力为
$$
f_x \rho dx dy dz
$$
$f_x$ 为单位质量上所受彻体力在 $x$ 轴方向分力。
因为是静止流体，流体微团受力平衡。
$x$ 轴方向力平衡方程为
$$
[p(x_0,y_0,z_0)-(\frac{\partial p}{\partial x})(\frac{dx}{2})]dx dy-[p(x_0,y_0,z_0)+(\frac{\partial p}{\partial x})(\frac{dx}{2})]dx dy+f_x \rho dx dy dz=0
$$
整理得
$$
\frac{\partial p}{\partial x}=\rho f_x
$$
$$
\frac{\partial p}{\partial y}=\rho f_y
$$
$$
\frac{\partial p}{\partial z}=\rho f_z
$$

$\because$ $p$ 全微分方程为
$$
dp=\frac{\partial p}{\partial x}dx+\frac{\partial p}{\partial y}dy+\frac{\partial p}{\partial z}dz
$$
$\therefore$
$$
dp=\rho(f_x dx+f_y dy+f_z dz)
$$
设==彻体力位函数==
$$
\varOmega=\varOmega(x,y,z)
$$
全微分为
$$
d \varOmega=\frac{\partial \varOmega}{\partial x}dx+\frac{\partial \varOmega}{\partial y}dy+\frac{\partial \varOmega}{\partial z}dz
$$
其中 $\frac{\partial \varOmega}{\partial x}=f_x$，$\frac{\partial \varOmega}{\partial y}=f_y$，$\frac{\partial \varOmega}{\partial z}=-f_z$
由上述关系得到
$$
dp=-\rho d \varOmega
$$
两边对 $x,y,z$ 三重积分得
$$
p=-\rho \varOmega+C(常数)
$$
$$
C=p+\rho \varOmega
$$
当已知某一点 A 处的压强 $p_a$ ，两点处彻体力位函数差 $\varOmega_a-\varOmega$ ，该静止流体密度 $\rho$ （处处相等）时，已知任一点彻体力位函数 $\varOmega$ 可求得该点压强
$$
p=p_a+\rho (\varOmega_a-\varOmega)
$$
推论： 流体内等压面必是彻体力的等位面。

大气

大气分层

底层大气

• 高度：海平面——85 km
• 特点：组分均匀，氮气占总体积 78.1%，氧气占总体积 21%

对流层

• 高度
  • 赤道：16~18 km
  • 中纬度地区：10~12 km
  • 两极：7~10 km
• 质量：占整个大气质量 75%
• 特点：有上下方向流动，有风暴、雷雨现象。随高度增加，空气温度快速下降。

对流顶层

过渡层，厚度数百米到一二千米。

平流层

• 高度：对流层~32 km
• 质量：约占大气层质量四分之一
• 特点：无气象，空气水平流动，温度保持常数（平均约 216.65 K）

中间大气层

• 高度：32~85 km
• 质量：1/3000
• 温度：先上升后下降，85 km 处可降到 106 K 以下。

高层大气

• 高度：85 km 以上
• 特点：组分不均匀，直接吸收太阳辐射

高温层

• 高度：85~500 km
• 温度：随高度升高温度上升，500 km 处白天可达 1370 K。
• 特点：直接受太阳短波辐射

外层大气

• 高度：500+ km，大气逐渐与星际空间融合
• 质量：$1/10^{11}$
• 特点：大气过于稀薄，不适合用温度定义。空气分子可逃逸入太空。

上层大气与电离层

• 上层大气受太阳短波辐射离解为电子和离子，形成电离层。
• 100 km 以上高空中，空气是良导体。
• 150 km 以上，空气过于稀薄，无法传递声音。

D 层

• 高度：60~80 km

E 层

• 高度：100~120 km

$F_1$ 层

• 高度：180~220 km

$F_2$ 层

• 高度：300~350 km

国际标准大气

航空工程中统一的大气压强、密度、温度等参数标准，按中纬度地区全年平均条件统计确定，称为国际标准大气。

流体运动学与动力学基础

流场

流场：充满运动流体的空间
流动参数：用以表示流体运动特征的物理量，入速度、密度、压强等。
流体力学方法：拉格朗日法，欧拉法

拉格朗日法

着眼于质点（运动）

• 研究流场各个质点的运动参数随时间变化规律和运动轨迹。
• 综合所有流体质点运动参数变化从而得到整个流场运动规律。

欧拉法

着眼于空间点（不动）

• 研究流体质点通过空间固定点时，运动参数随时间变化规律。
• 综合流场中所有空间点处运动参数变化情况，可得到整个流场运动规律。

欧拉法中，流场运动参数一般是空间点坐标和时间的函数。
以速度为例
$$
v=v(x,y,z,t)
$$
四个变量独立。
一般三维空间中，建立笛卡尔坐标系，将标量参数分解到 $x,y,z$ 轴方向分别分析。
$$
v_x=v_x(x,y,z,t)
$$
求导得加速度分量
$$
a_x=\frac{d v_x}{dt}=\frac{\partial v_x}{\partial t}+\frac{\partial v_x}{\partial x}\frac{dx}{dt}+\frac{\partial v_x}{\partial y}\frac{dy}{dt}+\frac{\partial v_x}{\partial z}\frac{dz}{dt}
$$
$\because$ $\frac{dx}{dt}=v_x,\frac{dy}{dt}=v_y,\frac{dz}{dt}=v_z$
$\therefore$
$$
a_x=\frac{\partial v_x}{\partial t}+v_x \frac{\partial v_x}{\partial x}+v_y \frac{\partial v_x}{\partial y}+v_z \frac{\partial v_x}{\partial z}
$$
由此可知，加速度是时间和位置的函数
$$
a_x=a_x(t,x,y,z)
$$

当地加速度

等式右边第一项表示空间固定点处的流体质点速度随时间变化率，称当地加速度。（速度与时间关系）
当地加速度是由流场中速度随时间的变化性引起的。

迁移加速度

后三项反映在同一瞬时，流体质点沿速度矢量方向从空间一点运动到相邻另一点速度变化率，称为迁移加速度。（速度与位移关系）
迁移加速度是由流畅的不均匀性引起的。

非定常流场

流场中至少存在一空间点的物理量随时间变化。

定常流场

流场中任意空间点处的物理量不随时间变化。

迹线

流场中标定的运动流体质点在一段时间内所经过所有空间点的集合，称为该流体质点迹线。

流线

在流场中每一空间点上都与速度矢量相切的曲线称为流线。
流线是同一时刻不同流体质点所组成的曲线，它给出该时刻不同流体质点的速度方向。
特点：

• 在定常流场中各流线不随时间变化。

• 非定常流场中存在随时间变化的流线。

• 定常流场中，经过某一空间点的流线，与所有经过该空间点的流体质点的迹线重合。

• 一般流线不相交（同一时刻同一空间点不存在两个速度方向）

• 在速度为 0 的空间点上，流线可以相交。通常称速度为 0 的空间点为驻点。

• 在速度无穷大的空间点上，流线可以相交，通常称速度无穷大的空间点为奇点。

• 流线相切，切点后两线重合。

• 流场中每一点都有流线通过，所有流线集合称为流线谱或简称流谱。

流线微分方程

设流线上某点 $M(x,y,z)$ 处速度为 $\vec{v}$ ，$M$ 点流线微段长 $ds$ ，在笛卡尔坐标系分解为 $v_x,v_y,v_z$ 和 $dx,dy,dz$ 。
流线任一点速度方向与流线切线方向相同，则
$$
\cos(\vec{v},\vec{i})=\frac{v_x}{v}=\frac{dx}{ds}
$$
$\vec{i}$ 为 $x$ 轴方向单位法向量，$y,z$ 轴同理。
$$
\frac{dx}{v_x}=\frac{dy}{v_y}=\frac{dz}{v_z}
$$
上式即为流线的微分方程式。
已知速度分布时，可求得流场中通过任一点的流线形状。

流管

在流场中一条不为流线的封闭曲线 C，过 C 上每一点作流线，由这些流线集合构成的管状曲面称为流管。

流体微团运动分析

运动形式

刚体运动

• 平移运动
• 绕轴转动

流体运动

• 平移运动
• 绕轴转动
• 变形运动
  • 直线变形
  • 剪切变形

二维分析

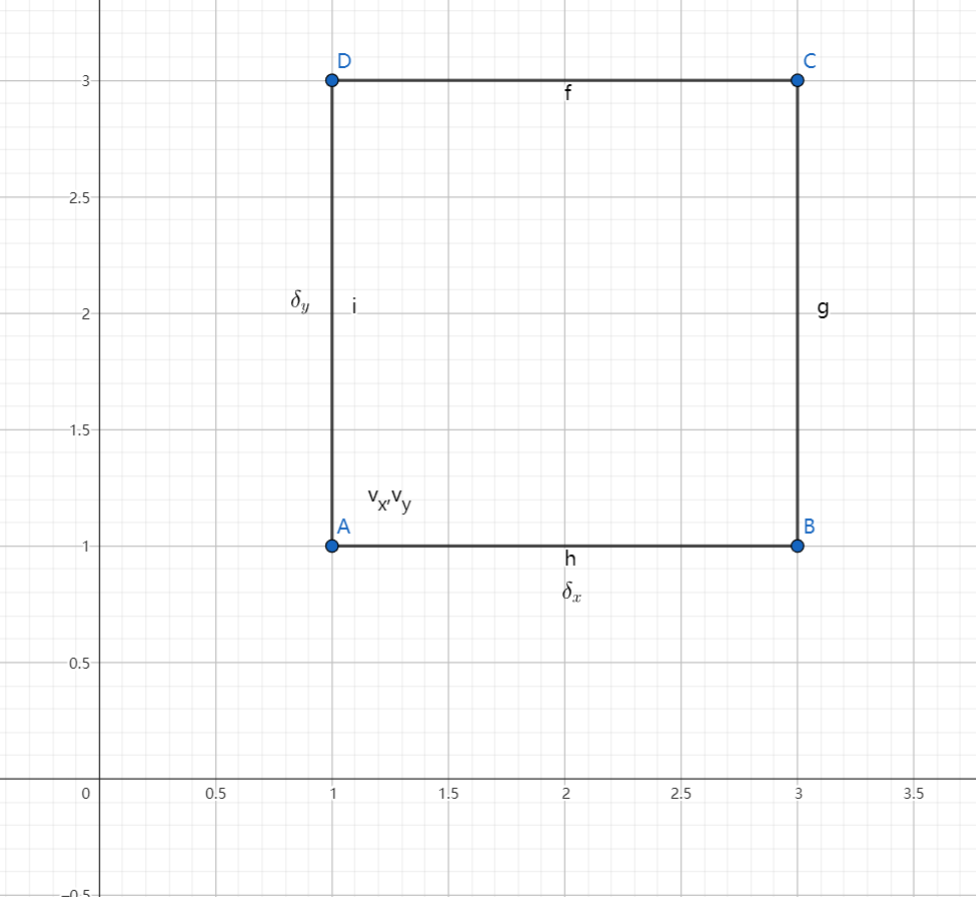
在流场中任取一矩形流体微团 ABCD，其两边的边长分别为 $\delta_x,\delta_y$ ，且均为小量。

设 $v_x,v_y$ 为 A 点处流体微团分速度，且分速度均为空间点坐标的连续函数，则 B, D 点速度可用泰勒级数在 A 点的展开表述。
$\because$ 流体微团边长足够小
$\therefore$ 二阶以上小量可忽略
$$
v_{Bx}=v_x+\frac{\partial v_x}{\partial x}\delta_x
$$
$$
v_{By}=v_y+\frac{\partial v_y}{x}\delta_x
$$
流体微团运动时，除了整体运动，B 相对于 A 点也有运动。
$x$ 轴方向相对运动速度 $v_{Bx}-v_x=\frac{\partial v_x}{\partial x}\delta_x$ ，$y$ 轴方向同理 $\frac{\partial v_x}{\partial x}\delta_x$ 。
D 相对于 A 运动速度为 $v_{Dx}-v_x=\frac{\partial v_x}{\partial y}\delta_y,v_{Dy}-v_y=\frac{\partial v_y}{\partial y}\delta_y$ 。

线变形运动

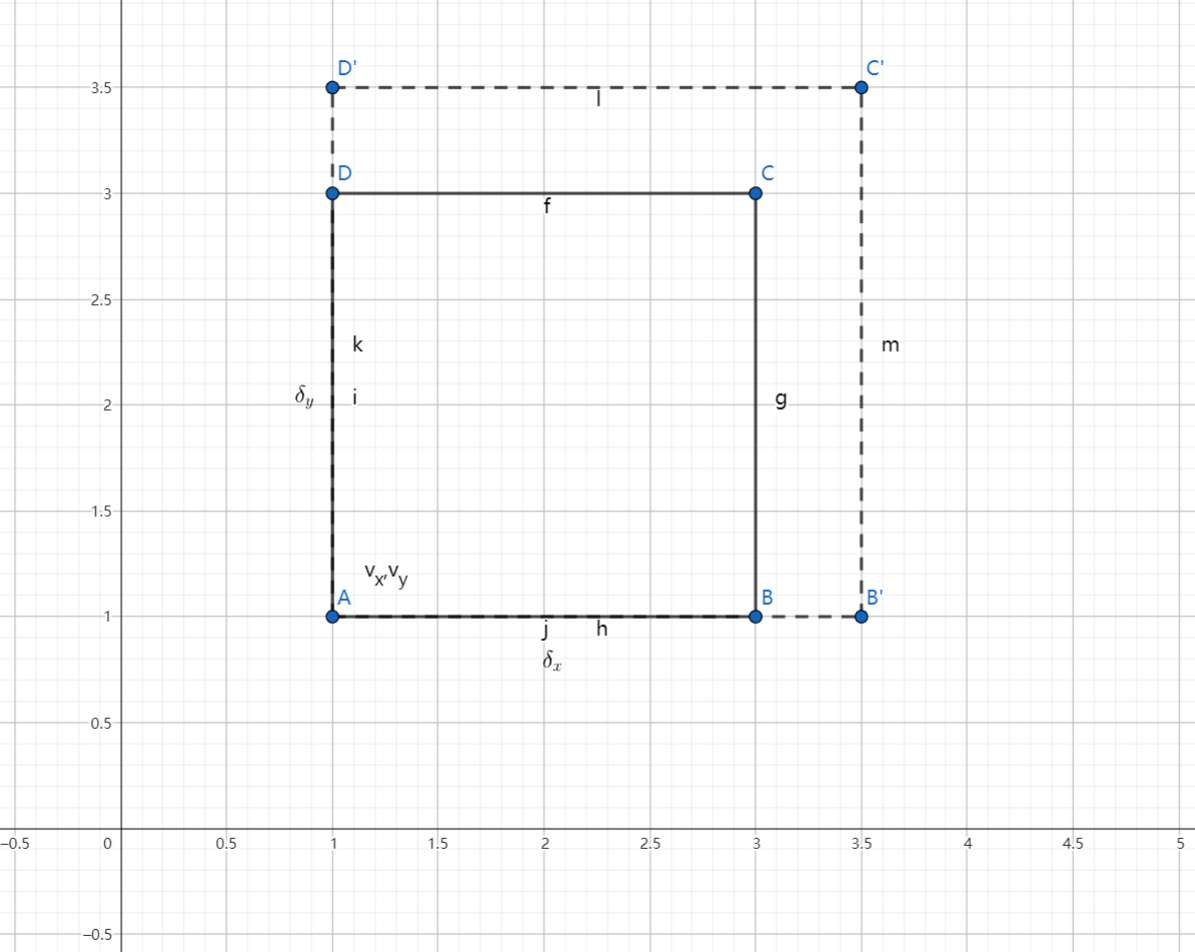
相对速度 $\frac{\partial v_x}{\partial x}\delta_x$ 和 $\frac{\partial v_y}{\partial y}\delta_y$ 是矩形 ABCD 边线的直线形变速度，时间 $dt$ 内
$$
AB'=AB+\frac{\partial v_x}{\partial x}\delta_x dt
$$
$$
AD'=AD+\frac{\partial v_y}{\partial y}\delta_y dt
$$
矩形面积相对变化率为
$$
\frac{d(\delta S)}{\delta S \cdot dt}=\frac{AB' \cdot CD'-AB \cdot CD}{AB \cdot CD \cdot dt}
$$
略去高阶小量后，
$$
\frac{d(\delta S)}{\delta S \cdot dt}=\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}
$$

拓展到三维空间后，同理可得
$$
\frac{d(\delta V)}{\delta V \cdot dt}=\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}
$$

角变形运动

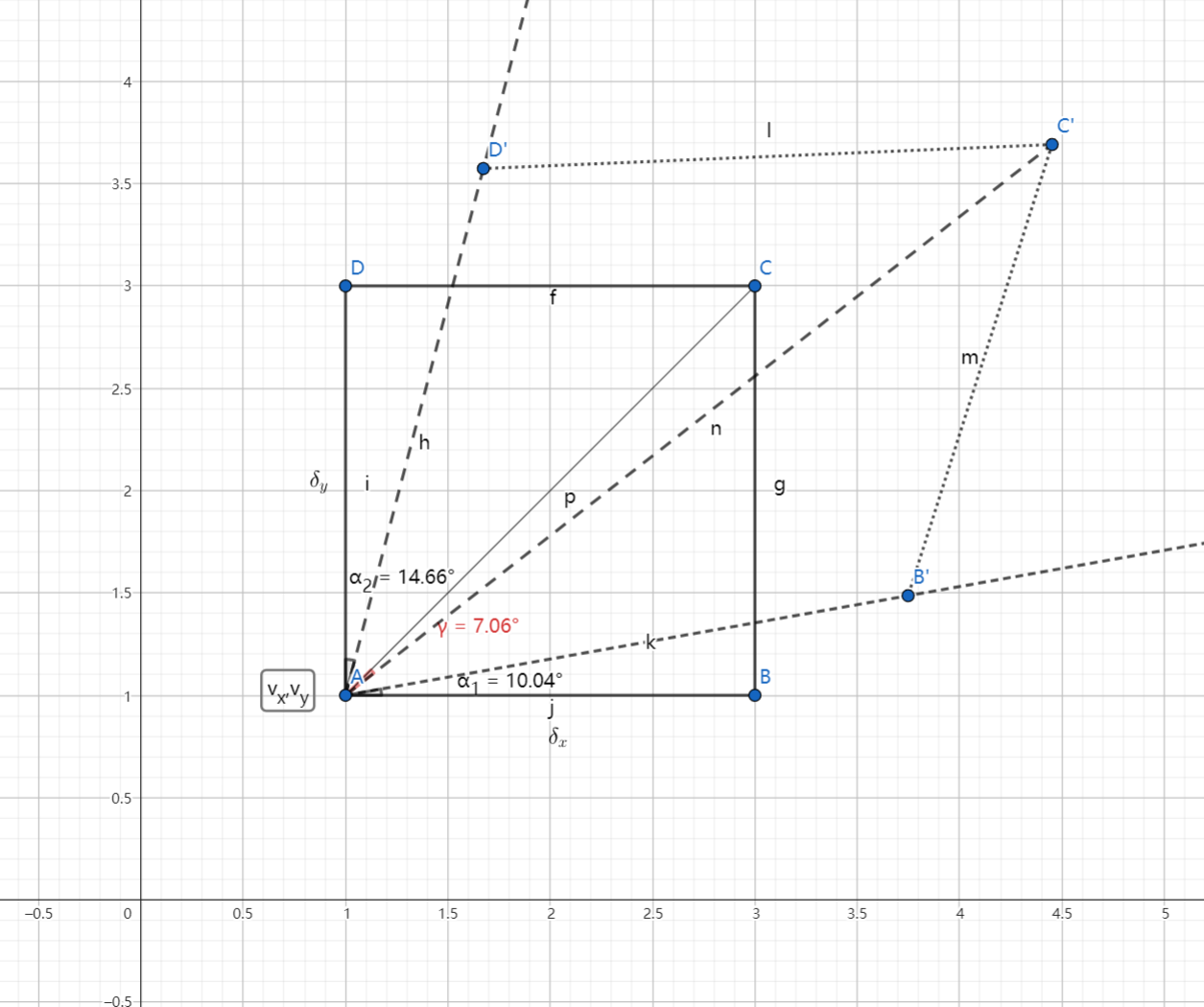
相对速度 $\frac{\partial v_y}{\partial x}\delta x,\frac{\partial v_x}{\partial y}\delta y$ 表示 AB 边和 AD 边绕 A 点的转动。
规定逆时针转动为正，
AB 边转动角速度
$$
\frac{d\alpha_1}{dt}=\frac{\partial v_y}{\partial x}\delta_x / \delta_x=\frac{\partial v_y}{\partial x}
$$
同理 AD 边转动角速度为
$$
\frac{d \alpha_2}{dt}=-\frac{\partial v_x}{\partial y}
$$

微团绕 $z$ 轴转动角速度

定义：微团在 $xOy$ 平面投影中两条互相垂直线绕 $z$ 轴转动角速度的平均值。（角速度和之半）
$$
\epsilon_z=\frac{1}{2}(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y})
$$

角变形率

定义：微团在 $xOy$ 平面投影中两条互相垂直线在单位时间内的夹角变化量之半。（角速度差之半）
$$
\gamma_z=\frac{1}{2}(\frac{\partial v_y}{\partial x}+\frac{\partial v_x}{\partial y})
$$
拓展到三维空间后，流体微团的三轴转动角速度和角变形率同理可求。
略。

散度

定义：各速度分量在其分量方向上的方向导数之和为速度矢量的三度。
$$
div \vec{v}=\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}
$$
物理意义：标定流体微团在运动过程中相对体积变化率。

==假设前提==：流体的密度没有发生变化（流体的运动视为不可压流）。
由一点发出的体积流量定义为
$$
\lim_{\delta V \to 0}\frac{体积流出量-体积流入量}{\delta V \cdot dt}=\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}
$$
等于单位时间内空间某一点处，单位体积控制体的体积净流出量，等于流体微团在运动中体积相对变化率。

旋度

定义：旋转角速度的两倍。
$$
\vec{\omega}=curl \vec{v}=(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z})\vec{i}+(\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x})\vec{j}+(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y})\vec{k}
$$

速度位

在流体力学中, 可根据流体微团是否有旋转运动, 而将流体运动分为

• 有旋运动
• 无旋运动

当把流动看作无旋运动时，$\omega=0$ ，
$$
\begin{cases}
\frac{\partial v_z}{\partial y}=\frac{\partial v_y}{\partial z} \\
\frac{\partial v_x}{\partial z}=\frac{\partial v_z}{\partial x} \\
\frac{\partial v_y}{\partial x}=\frac{\partial v_x}{\partial y} \\
\end{cases}
$$
上述方程组是 $v_xdx+v_ydy+v_zdz$ 构成某函数 $\phi(x,y,z)$ 全微分的充要条件。即
$$
d \phi=v_xdx+v_ydy+v_zdz=\frac{\partial \phi}{\partial x}dx+\frac{\partial \phi}{\partial y}dy+\frac{\partial \phi}{\partial z}dz
$$
$\phi$ 称为速度位或速度位函数。
$$
\begin{cases}
v_x=\frac{\partial \phi}{\partial x}\\
v_y=\frac{\partial \phi}{\partial y}\\
v_z=\frac{\partial \phi}{\partial z}\\
\end{cases}
$$
使用柱极坐标时，
$$
\phi=\phi(r,\theta,z)
$$
$$
\begin{cases}
v_r=\frac{\partial \phi}{\partial r}\\
v_\theta=\frac{\partial \phi}{\partial \theta}\\
v_z=\frac{\partial \phi}{\partial z}\\
\end{cases}
$$

基本物理量

应力 ：单位面积上的力称为应力

标量

压强

密度

温度

粘性系数

矢量

流动速度

剪应力

理想气体状态方程

$$
pV=nRT
$$
$R=8.314J \cdot mol^{-1} \cdot K^{-1}$ 为理想摩尔气体常数。
$$
p=\frac{n \cdot M}{V}\frac{R}{M} T
$$
$$
n(物质的量) \cdot M(摩尔质量)=m(质量)
$$
$$
p=\rho R' T
$$
$$
R'=\frac{R}{M}
$$
$R'$ 为==比气体常数==。
理想空气 $R'=287J/(kg \cdot K)$

空气动力及力矩

空气动力 $R$：Resultant

空气对物体的力

• 压力 $p$ ：Pressure
• 剪应力 $\tau$ ：Shear stress

压力与剪应力的合力即为空气对物体作用力，空气动力。

风轴系

• 升力 $L$ ：Lift，竖直分力
• 阻力 $D$ ：Drag，水平分力

自由来流（自由流）

$$
V_{\infty}
$$
自由流是指飞机前未经扰动的来流，也即没有飞机等干扰时，空气的自然流动现象。
升力与阻力的方向由自由来流方向决定。

迎角（攻角）

$$
\alpha
$$
迎角（英语：Angle of attack，缩写为AOA，常用希腊字母α表示）为空气动力学名词，为机翼之翼弦与自由流（或是相对风流的方向）之夹角；如为飞机迎角，定义则为机轴对相对风流之夹角。当机翼向上为正迎角，向下则为负迎角。

体轴系

• 法向力 $N$：Normal，垂直于机翼方向
• 轴向力 $A$：Axial，平行于机翼方向

力矩 $M$：Moment

让飞机抬头的力矩为正，让飞机低头力矩为负。

动压 $q$

自由来流 $V_{\infty},\rho_{\infty}$ 产生的动压
$$
q_{\infty}=\frac{1}{2}\rho_{\infty}V_{\infty}^2
$$
单位为 $Pa$ ，同压强

特征几何尺寸 $S$

对三维物体来说是面积，对二位物体来说是周长。

无量纲参数

三维物体常用大写 $C$ ，二维物体常用小写 $c$ 。

升力系数

$$
C_L=\frac{L}{q_{\infty}S}
$$

阻力系数

$$
C_D=\frac{D}{q_{\infty}S}
$$

法向力系数

$$
C_N=\frac{N}{q_{\infty}S}
$$

轴向力系数

$$
C_A=\frac{A}{q_{\infty}S}
$$

空气动力系数

$$
C_R=\frac{R}{q_{\infty}S}
$$

力矩系数

$$
C_M=\frac{\vec{M}}{\vec{r} \times \vec{q_{\infty}}S}
$$

压力系数

$p$：某点静压
$p_{\infty}$：自由来流静压
$$
C_p=\frac{p-p_{\infty}}{q_{\infty}}
$$

摩擦力系数

$\tau$：某点剪应力，即剪应力对面积导数。量纲同压强。
$$
C_f=\frac{\tau}{q_{\infty}}
$$

两个中心

压力中心（压心）

压力中心（Pressure Center）：流体中的平面或曲面所受流体压力的合力的作用线同该平面或曲面的交点。空气动力 $R$ 对此点力矩为 $\vec{0}$。

空气动力中心（气动中心，焦点）

空气动力中心（英语：aerodynamic center，简称 AC）在空气动力学 中是指翼型 上的一个定点，绕该点的俯仰力矩不随迎角 的改变而变化，即
$$
\frac{d C_M}{d \alpha}=0
$$

气动中心与压力中心的区别

压力中心是力系合成到一个特殊点时，使得这个点的合力矩为0的点，压力中心在气动中心的后面；而气动中心是使得合力矩不变的点。

压力中心的位置随着迎角的改变而改变，当迎角增大，升力增大，压力中心前移，这同时使得压力中心与气动中心的距离缩短，增大的升力与缩短力臂乘积刚好是不变的力矩，这也正是气动中心的定义所要求的。