实现哈夫曼树的编码和译码
a. 问题分析
目标:
实现哈夫曼树的编码和译码。
问题:
- 构建哈夫曼树的过程是否正确?
- 是否正确生成了哈夫曼编码?
- 是否正确进行了哈夫曼编码和译码的过程?
- 是否能够处理频率相同的字符?
b. 算法设计
1. 构建哈夫曼树:
- 根据输入的文本,计算字符的频率。
- 使用优先队列(最小堆)构建哈夫曼树。
输入: 字符频率的映射 frequencies。
输出: 哈夫曼树的根节点 root。
HuffmanNode* buildHuffmanTree(map<char, int>& frequencies) {
// 1. 创建优先队列(最小堆)用于构建哈夫曼树
priority_queue<HuffmanNode*, vector<HuffmanNode*>, CompareNodes> minHeap;
// 2. 创建叶子节点并加入最小堆
for (auto& entry : frequencies) {
HuffmanNode* node = new HuffmanNode(entry.first, entry.second);
minHeap.push(node);
}
// 3. 构建哈夫曼树
while (minHeap.size() > 1) {
HuffmanNode* left = minHeap.top();
minHeap.pop();
HuffmanNode* right = minHeap.top();
minHeap.pop();
HuffmanNode* internalNode = new HuffmanNode('$', left->frequency + right->frequency);
internalNode->left = left;
internalNode->right = right;
minHeap.push(internalNode);
}
// 4. 返回哈夫曼树的根节点
return minHeap.top();
}2. 生成哈夫曼编码:
- 使用递归方式遍历哈夫曼树,生成每个字符的哈夫曼编码。
输入: 哈夫曼树的根节点root,空的字符串code,空的映射huffmanCodes。
输出: 映射huffmanCodes包含字符到哈夫曼编码的映射。
void generateHuffmanCodes(HuffmanNode* root, string code, map<char, string>& huffmanCodes) {
// 1. 递归终止条件:遇到叶子节点
if (root == nullptr) {
return;
}
// 2. 如果是叶子节点,将字符和对应的哈夫曼编码存入映射
if (root->data != '$') {
huffmanCodes[root->data] = code;
}
// 3. 递归生成左子树和右子树的哈夫曼编码
generateHuffmanCodes(root->left, code + "0", huffmanCodes);
generateHuffmanCodes(root->right, code + "1", huffmanCodes);
}3. 哈夫曼编码:
- 遍历输入文本,根据生成的哈夫曼编码替代每个字符。
输入: 原始文本text,哈夫曼编码的映射huffmanCodes。
输出: 哈夫曼编码后的文本encodedText。
string huffmanEncode(string text, map<char, string>& huffmanCodes) {
string encodedText = "";
// 遍历原始文本,根据映射替代每个字符
for (char c : text) {
encodedText += huffmanCodes[c];
}
return encodedText;
}4. 哈夫曼译码:
- 遍历哈夫曼编码,根据编码的'0'和'1'分别访问哈夫曼树的左子树和右子树,直到达到叶子节点,将叶子节点的字符添加到译码结果中。
输入: 哈夫曼编码后的文本encodedText,哈夫曼树的根节点root。
输出: 哈夫曼译码后的文本decodedText。
string huffmanDecode(string encodedText, HuffmanNode* root) {
string decodedText = "";
HuffmanNode* current = root;
// 遍历哈夫曼编码
for (char bit : encodedText) {
// 根据 '0' 和 '1' 访问左子树或右子树
if (bit == '0') {
current = current->left;
} else {
current = current->right;
}
// 如果遇到叶子节点,将字符加入译码结果,并重置为根节点
if (current->data != '$') {
decodedText += current->data;
current = root;
}
}
return decodedText;
}c. 数据结构设计
- HuffmanNode 结构体:
- 存储字符、频率,以及左右子节点指针。
- CompareNodes 结构体:
- 用于定义节点比较的规则,构建最小堆。
- std::priority_queue:
- 使用最小堆存储 HuffmanNode 指针,用于构建哈夫曼树。
- std::map\<char, int>:
- 用于存储字符频率。
d. 调试过程
-
构建哈夫曼树:
- 检查频率计算是否正确。
- 检查最小堆的构建是否按照预期进行。
-
生成哈夫曼编码:
- 通过手动计算部分编码,验证生成的哈夫曼编码是否正确。
-
哈夫曼编码和译码:
- 使用简单的测试用例,检查编码和译码的正确性。
- 特别关注频率相同字符的情况,确保其相对顺序保持不变。
e. 输出结果
运行程序并使用测试用例(例如输入 "zhubingqianwoxihuanni")检查输出结果。确保输出包括哈夫曼编码、编码后的文本和译码后的文本,并验证其正确性。
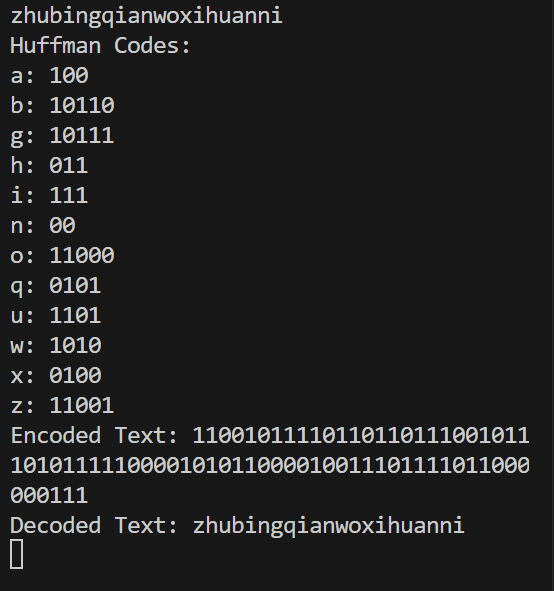
以下是输入text为"hello world"时的输出结果
Huffman Codes:
d: 00
r: 010
$: 011
w: 1000
e: 1001
o: 101
l: 110
h: 1110
: 1111
Encoded Text: 111000110010100010010010110111010010011110111100
Decoded Text: hello worldf. 源代码
#include <iostream>
#include <queue>
#include <map>
#include <string>
using namespace std;
// 定义哈夫曼树的节点结构
struct HuffmanNode {
char data;
int frequency;
HuffmanNode *left, *right;
HuffmanNode(char d, int freq) : data(d), frequency(freq), left(nullptr), right(nullptr) {}
};
// 用于比较两个节点的优先级
struct CompareNodes {
bool operator()(HuffmanNode* a, HuffmanNode* b) {//重载'+'运算符
return a->frequency > b->frequency;
}
};
// 构建哈夫曼树
HuffmanNode* buildHuffmanTree(map<char, int>& frequencies) {
priority_queue<HuffmanNode*, vector<HuffmanNode*>, CompareNodes> minHeap;
//优先队列模板,元素类型HuffmanNode*,容器类型vector<HuffmanNode*>,比较规则函数CompareNodes
// 创建叶子节点,并加入最小堆
for (auto& entry : frequencies) {//auto,自动判断entry类型为frequencies里的键值对
HuffmanNode* node = new HuffmanNode(entry.first, entry.second);
minHeap.push(node);//入队
}
//priority_queue会自动维护队列优先级
// 构建哈夫曼树
while (minHeap.size() > 1) {//优先队列只剩下一个节点时为根节点,退出循环
HuffmanNode* left = minHeap.top();
minHeap.pop();
HuffmanNode* right = minHeap.top();
minHeap.pop();
HuffmanNode* internalNode = new HuffmanNode('$', left->frequency + right->frequency);
//创建两个子节点的根节点,frequency为子节点的frequency之和
internalNode->left = left;
internalNode->right = right;
minHeap.push(internalNode);//将该根节点加入minHeap重新排列
}
//生成Huffman树,所有非叶子节点data为'$'
// 返回根节点
return minHeap.top();
}
// 递归地生成哈夫曼编码
void generateHuffmanCodes(HuffmanNode* root, string code, map<char, string>& huffmanCodes) {
if (root == nullptr) {
return;
}
if (root->data != '$') {//读到叶子节点
huffmanCodes[root->data] = code;//该字符编码为code
}
generateHuffmanCodes(root->left, code + "0", huffmanCodes);
generateHuffmanCodes(root->right, code + "1", huffmanCodes);
//递归实现,访问左子树+0,访问右子树+1
}
// 哈夫曼编码
string huffmanEncode(string text, map<char, string>& huffmanCodes) {
string encodedText = "";//初始化result为空字符串
for (char c : text) {
encodedText += huffmanCodes[c];//根据字符c加入相应的哈夫曼编码
}
return encodedText;//返回结果
}
// 哈夫曼译码
string huffmanDecode(string encodedText, HuffmanNode* root) {
string decodedText = "";//初始化译码结果为空字符串
HuffmanNode* current = root;
for (char bit : encodedText) {
if (bit == '0') {//读到'0'访问左子树,读到'1'访问右子树
current = current->left;
} else {
current = current->right;
}
if (current->data != '$') {//读到叶子节点,确定该段哈夫曼编码译码结果
decodedText += current->data;
current = root;//返回根节点继续下次译码
}
}
return decodedText;
}
int main() {
//string text = "hello world";
string text;
cin>>text;
map<char, int> frequencies;
// 计算字符频率
for (char c : text) {
frequencies[c]++;
}
// 构建哈夫曼树
HuffmanNode* root = buildHuffmanTree(frequencies);
// 生成哈夫曼编码
map<char, string> huffmanCodes;
generateHuffmanCodes(root, "", huffmanCodes);
// 打印哈夫曼编码
cout << "Huffman Codes:" << endl;
for (auto& entry : huffmanCodes) {
cout << entry.first << ": " << entry.second << endl;//打印键值对
}
// 哈夫曼编码
string encodedText = huffmanEncode(text, huffmanCodes);
cout << "Encoded Text: " << encodedText << endl;
// 哈夫曼译码
string decodedText = huffmanDecode(encodedText, root);
cout << "Decoded Text: " << decodedText << endl;
return 0;
}
总结
通过测试,确保程序正确实现了哈夫曼树的构建、编码和译码功能。特别注意频率相同字符的处理,确保其相对顺序不变。在构建哈夫曼树时,使用最小堆保证了节点按照频率的升序排列。
排序二叉树的构建和节点删除
a 问题分析
本实验的目标是实现基于排序二叉树的节点插入、中序遍历、删除整个树以及删除单独某个节点的功能。具体要求包括使用struct实现节点,实现插入节点和删除节点的功能。
b 算法设计
插入节点算法设计
插入节点的算法是一个递归算法。根据节点值与当前节点值的比较,选择插入到左子树或右子树。如果当前子树为空,创建一个新节点并返回;否则,递归调用插入函数。
TreeNode* insert(TreeNode* root, int val) {
if (root == nullptr) {
return new TreeNode(val);
}
if (val <= root->data) {
root->left = insert(root->left, val);
} else if (val > root->data) {
root->right = insert(root->right, val);
}
return root;
}构建排序二叉树算法设计
构建排序二叉树的算法使用了插入节点算法。遍历输入序列,对每个元素调用插入节点函数,不断更新根节点,最终得到一个排序二叉树。
TreeNode* buildTree(int input[], int size) {
TreeNode* root = nullptr;
for (int i = 0; i < size; ++i) {
root = insert(root, input[i]);
}
return root;
}中序遍历算法设计
中序遍历算法用于输出排序二叉树的节点值,以验证树的构建是否正确。
void inorderTraversal(TreeNode* node) {
if (node != nullptr) {
inorderTraversal(node->left);
cout << node->data << " ";
inorderTraversal(node->right);
}
}删除整个树算法设计
删除整个树的算法是一个递归算法。递归调用删除函数,删除左子树和右子树,最后删除当前节点。
void deleteTree(TreeNode* node) {
if (node != nullptr) {
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
}删除单独某个节点算法设计
删除单独某个节点的算法是一个递归算法。根据节点值与待删除值的比较,选择在左子树或右子树中进行删除。如果找到匹配的节点,分三种情况处理:节点没有子节点、节点有一个子节点、节点有两个子节点。
TreeNode* deleteNode(TreeNode* root, int val) {
if (root == nullptr) {
return root;
}
// 找到匹配节点
if (val < root->data) {
root->left = deleteNode(root->left, val);
} else if (val > root->data) {
root->right = deleteNode(root->right, val);
} else {
// 节点有一个或无子节点
if (root->left == nullptr) {
TreeNode* temp = root->right;
delete root;
return temp;
} else if (root->right == nullptr) {
TreeNode* temp = root->left;
delete root;
return temp;
}
// 节点有两个子节点,找到右子树的最小节点
TreeNode* minRight = root->right;
while (minRight->left != nullptr) {
minRight = minRight->left;
}
// 复制最小节点的值到当前节点
root->data = minRight->data;
// 删除右子树中的最小节点
root->right = deleteNode(root->right, minRight->data);
}
return root;
}
// 删除单独某个节点的接口函数
TreeNode* deleteSingleNode(TreeNode* root, int val) {
TreeNode* nodeToDelete = findNode(root, val);
if (nodeToDelete != nullptr) {
root = deleteNode(root, val);
}
return root;
}c 数据结构设计
节点结构
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};d 调试过程
在调试过程中,首先确保 deleteSingleNode 函数能够正确执行。通过删除单独某个节点后,使用中序遍历验证排序二叉树的节点值,以确保删除操作的正确性。最后,通过输出验证整个实现的正确性。
e 输出结果
针对输入序列 7, 5, 9, 2, 5, 2, 6, 3, 7, 0,实验的输出结果如下:
排序二叉树: 0 2 2 3 5 5 6 7 7 9
删除节点 3 后的排序二叉树: 0 2 2 5 5 6 7 7 9
删除单独节点 5 后的排序二叉树: 0 2 2 6 7 7 9 这个输出结果表明删除单独某个节点的功能已经添加,并且在删除节点 5 后,中序遍历输出排序二叉树的节点值,验证删除操作的正确性。
f 源代码
#include <iostream>
using namespace std;
// 定义二叉树节点
struct TreeNode {
int data;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
// 插入节点到排序二叉树
TreeNode* insert(TreeNode* root, int val) {
if (root == nullptr) {
return new TreeNode(val);
}
if (val <= root->data) {
root->left = insert(root->left, val);
} else if (val > root->data) {
root->right = insert(root->right, val);
}
return root;
}
// 中序遍历
void inorderTraversal(TreeNode* node) {
if (node != nullptr) {
inorderTraversal(node->left);
cout << node->data << " ";
inorderTraversal(node->right);
}
}
// 删除整个树
void deleteTree(TreeNode* node) {
if (node != nullptr) {
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
}
// 查找节点值为val的节点
TreeNode* findNode(TreeNode* root, int val) {
if (root == nullptr || root->data == val) {
return root;
}
if (val < root->data) {
return findNode(root->left, val);
} else {
return findNode(root->right, val);
}
}
// 删除单独某个节点
TreeNode* deleteNode(TreeNode* root, int val) {
if (root == nullptr) {
return root;
}
// 找到匹配节点
if (val < root->data) {
root->left = deleteNode(root->left, val);
} else if (val > root->data) {
root->right = deleteNode(root->right, val);
} else {
// 节点有一个或无子节点
if (root->left == nullptr) {
TreeNode* temp = root->right;
delete root;
return temp;
} else if (root->right == nullptr) {
TreeNode* temp = root->left;
delete root;
return temp;
}
// 节点有两个子节点,找到右子树的最小节点
TreeNode* minRight = root->right;
while (minRight->left != nullptr) {
minRight = minRight->left;
}
// 复制最小节点的值到当前节点
root->data = minRight->data;
// 删除右子树中的最小节点
root->right = deleteNode(root->right, minRight->data);
}
return root;
}
// 删除单独某个节点的接口函数
TreeNode* deleteSingleNode(TreeNode* root, int val) {
TreeNode* nodeToDelete = findNode(root, val);
if (nodeToDelete != nullptr) {
root = deleteNode(root, val);
}
return root;
}
int main() {
int input[] = {7, 5, 9, 2, 5, 2, 6, 3, 7, 0};
TreeNode* root = nullptr;
// 构建排序二叉树
for (int i = 0; i < 10; ++i) {
root = insert(root, input[i]);
}
// 显示排序二叉树
cout << "排序二叉树: ";
inorderTraversal(root);
cout << endl;
// 删除节点 3 后的排序二叉树
int nodeToDelete = 3;
root = deleteNode(root, nodeToDelete);
cout << "删除节点 " << nodeToDelete << " 后的排序二叉树: ";
inorderTraversal(root);
cout << endl;
// 删除单独节点 5 后的排序二叉树
int singleNodeToDelete = 5;
root = deleteSingleNode(root, singleNodeToDelete);
cout << "删除单独节点 " << singleNodeToDelete << " 后的排序二叉树: ";
inorderTraversal(root);
cout << endl;
// 删除整个树
deleteTree(root);
return 0;
}
