Fibonacci序列
问题分析
要正确实现程序的递归调用和返回,必须解决参数的传递和返回地址问题。具体地说,进行调用时,每递归一次都要给所有参变量重新分配储存空间,并要把前一次调用的实参和本次调用后的返回地址保留。
算法设计
算法描述如下:
int Fib(int n){
int fib;
if(n==0) fib=0;
else if(n==1) fib=1;
else fib=Fib(n-1)+Fib(n-2);
return fib;
}数据结构设计
用栈去分配和管理储存空间,系统在每次执行调用过程的语句时需要开辟一个“工作记录”,用以保存调用前过程中所有参变量的值及调用后的返回地址,将此工作记录存于栈中,以便在返回时能在栈顶找到正确的信息。
调试过程
在每次调用函数的时候,将传入的参数进行输出,可以更直观地看到栈的调用过程。
以最开始Fib(2)的递归调用为例,程序先将Fib(5)、Fib(4)…Fib(1)储存到栈中,当n\==1时,将值返回上一个地址中,同理也将n\==0时的值返回,这样Fib(2)的值便有了,再返回到Fib(2)的上一级Fib(3)中。
输出结果
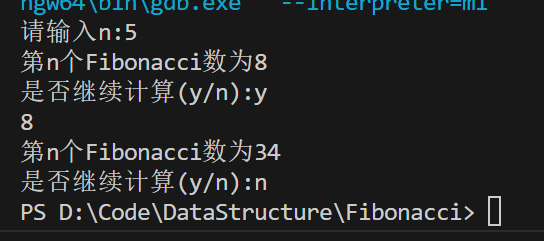
源代码
#include<bits/stdc++.h>
using namespace std;
int Fibonacci(int n){
int fib;
if(n==0){
fib=0;
}else if(n==1){
fib=1;
}else if(n==2){
fib=2;
}else{
fib=Fibonacci(n-1)+Fibonacci(n-2);
}
return fib;
}
int main(){
int n=0;
cout<<"请输入n:";
start:
cin>>n;
cout<<"第n个Fibonacci数为"<<Fibonacci(n)<<endl;
cout<<"是否继续计算(y/n):";
char choice;
choice:
cin>>choice;
if(choice=='y'||choice=='Y'){
goto start;
}else if(choice=='n'||choice=='N'){
return 0;
}else{
cout<<"输入错误,请重新输入:";
goto choice;
}
return 0;
}划分子集问题
问题分析
问题要求我们将一个集合中划分成互不相交的子集,使任何子集上的元素无任何冲突,且划分的子集数较少。此类问题常用在日程安排上。
算法设计
冲突关系首先通过一个二维数组表示出来,有冲突关系则赋值1,无冲突则赋值0。通过循环筛选法对其划分,即从第一个元素开始,先将元素1单独拿出,逐个判断其他元素是否和拿出的所有元素有冲突关系,无冲突则拿出元素,并划为一组。这样循环一周,所有互相无冲突关系的已被划为一组,循环此操作,即可完成划分要求。
数据结构设计
通过一个循环队列来储存数据,每次循环一周,不断迭代数据,不需要开辟新的存储空间。
调试过程
输出结果
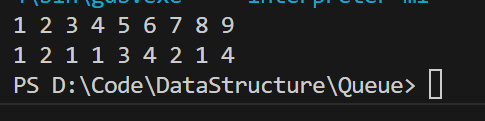
源代码
#include<bits/stdc++.h>
using namespace std;
int newr[9];
void DivideIntoGroup(int n,int R[][9],int cp[],int result[])
{
int front,rear,group,pre,I,i;
front=n-1;
rear=n-1;
for(i=0;i<n;i++)
{
newr[i]=0;
cp[i]=i+1;
}
group=1;
pre=0;
do
{
front=(front+1)%n;
I=cp[front];
if(I<pre)
{
group=group+1;
result[I-1]=group;
for(i=0;i<n;i++)
{
newr[i]=R[I-1][i];
}
}
else
{
if(newr[I-1]!=0)
{
rear=(rear+1)%n;
cp[rear]=I;
}
else
{
result[I-1]=group;
for(i=0;i<n;i++)
{
newr[i]+=R[I-1][i];
}
}
}
pre=I;
}while(rear!=front);
}
int main(){
int result[9],cp[9];
int R[9][9]=
{
{0,1,0,0,0,0,0,0,0},
{1,0,0,0,1,1,0,1,1},
{0,0,0,0,0,1,1,0,0},
{0,0,0,0,1,0,0,0,1},
{0,1,0,1,0,1,1,0,1},
{0,1,1,0,1,0,1,0,0},
{0,0,1,0,1,1,0,0,0},
{0,1,0,0,0,0,0,0,0},
{0,1,0,1,1,0,0,0,0},
};
DivideIntoGroup(9,R,cp,result);
for(int i=0;i<9;i++)
{
cout<<i+1<<" ";
}
cout<<endl;
for(int i=0;i<9;i++)
{
cout<<result[i]<<" ";
}
return 0;
}